21、剑指 Offer 10- II. 青蛙跳台阶问题
目录
一、题目
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:2
示例 2:
输入:n = 7
输出:21
示例 3:
输入:n = 0
输出:1
提示:
0 <= n <= 100
注意:本题与主站 70 题相同:https://leetcode-cn.com/problems/climbing-stairs/
二、解法
2.1、动态规划
核心思路
此类求 多少种可能性 的题目一般都有 递推性质 ,即 f(n) 和 f(n-1) ... f(1) 之间是有联系的。
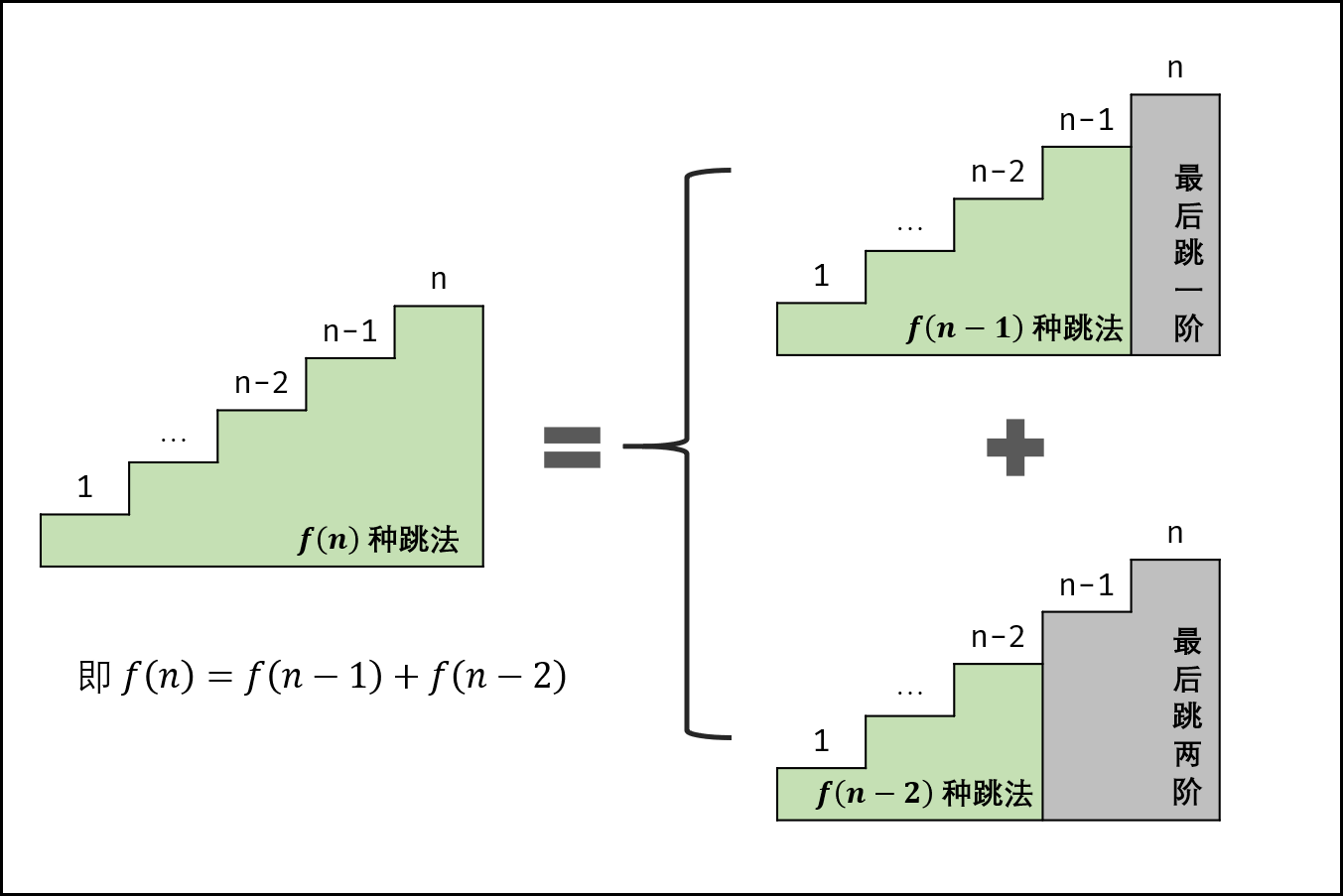
设跳上 n 级台阶有 f(n) 种跳法。在所有跳法中,青蛙的最后一步只有两种情况: 跳上 1 级或 2 级台阶。
- 当为
1级台阶: 剩n-1个台阶,此情况共有f(n-1)种跳法; - 当为
2级台阶: 剩n-2个台阶,此情况共有f(n-2)种跳法。
f(n) 为以上两种情况之和,即 f(n)=f(n-1)+f(n-2) ,以上递推性质为斐波那契数列。本题可转化为 求斐波那契数列第 n 项的值。与 面试题10- I. 斐波那契数列 等价,唯一的不同在于起始数字不同。
-
青蛙跳台阶问题:
f(0)=1 , f(1)=1 , f(2)=2; -
斐波那契数列问题:
f(0)=0 , f(1)=1 , f(2)=1。
本题如果使用递归实现,时间会超限,因此使用循环。
复杂度分析
时间复杂度:O(N) , 计算 f(n) 需循环 n 次,每轮循环内计算操作使用 O(1) 。
空间复杂度:O(1) ,几个标志变量使用常数大小的额外空间。
Code
class Solution {
public int numWays(int n) {
int a = 1, b = 1, c;
for (int i = 0; i < n; i++) {
c = (a + b) % 1000000007;
a = b;
b = c;
}
return a;
}
}