22、剑指 Offer 37. 序列化二叉树
一、题目
剑指 Offer 37. 序列化二叉树 难度困难236收藏分享切换为英文接收动态反馈
请实现两个函数,分别用来序列化和反序列化二叉树。
你需要设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
**提示:**输入输出格式与 LeetCode 目前使用的方式一致,详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。
示例:
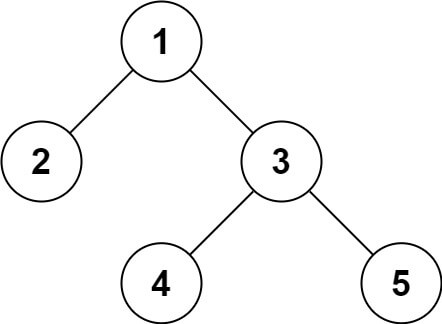
输入:root = [1,2,3,null,null,4,5]
输出:[1,2,3,null,null,4,5]
注意:本题与主站 297 题相同:https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree/
二、解法
2.1、BFS / 层序遍历
核心思路
通常使用的前序、中序、后序、层序遍历记录的二叉树的信息不完整,即唯一的输出序列可能对应着多种二叉树可能性。题目要求的 序列化 和 反序列化 是 可逆操作 。因此,序列化的字符串应携带 完整的二叉树信息 。
观察题目示例,序列化的字符串实际上是二叉树的 “层序遍历”(BFS)结果,本文也采用层序遍历。
为完整表示二叉树,将叶节点下的 null 也记录。在此基础上,对于列表中任意某节点 node ,其左子节点 node.left 和右子节点 node.right 在序列中的位置都是 唯一确定的。
因此,序列化使用层序遍历实现,借助队列,对二叉树做层序遍历,并将越过叶节点的 null 也打印出来。
按照层序遍历的规则,也可实现反序列化。利用队列按层构建二叉树,借助一个指针 i 指向节点 node 的左、右子节点,每构建一个 node 的左、右子节点,指针 i 就向右移动 1 位。
复杂度分析
时间复杂度:O(n),在序列化和反序列化函数中,我们只访问每个节点一次,因此时间复杂度为 O(n),其中 n 是节点数,即树的大小。
空间复杂度:最差情况下,队列 queue 同时存储 (N+1)/2 个节点,因此使用 O(N) 额外空间。
Code
class Codec {
// 序列化
public String serialize(TreeNode root) {
// 特例处理
if (root == null) return "[]";
// 结果
StringBuilder result = new StringBuilder("[");
// 队列 包含根节点 root
Queue<TreeNode> queue = new LinkedList<TreeNode>() {{
add(root);
}};
// 当队列不为空时, 循环处理
while (!queue.isEmpty()) {
// 节点出队, 记为 node
TreeNode node = queue.poll();
// 若 node 不为 null
if (node != null) {
// 将 node.val 拼接到结果中
result.append(node.val + ",");
// 将 node 的左, 右子节点加入队列, 等待下一轮处理
queue.add(node.left);
queue.add(node.right);
} else {
// 将 null 拼接到结果中
result.append("null,");
}
}
// 删除末尾的 , 号
result.deleteCharAt(result.length() - 1);
// 拼接 ] 号
result.append("]");
// 将 StringBuilder 转为 String
return result.toString();
}
// 反序列化
public TreeNode deserialize(String data) {
// 特例处理
if (data.equals("[]")) return null;
// 序列化列表 - 先去掉首尾中括号,再用逗号分割为字符串数组
String[] vals = data.substring(1, data.length() - 1).split(",");
// 根节点 root - 值为 vals[0]
TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
// 队列 - 包含根节点 root
Queue<TreeNode> queue = new LinkedList<TreeNode>() {{
add(root);
}};
// 按层构建, 指针 i
int i = 1;
// 当队列不为空时, 按层循环构建整棵树
while (!queue.isEmpty()) {
// 节点出队, 记为 node
TreeNode node = queue.poll();
// 若 vals[i] 不为 null
if (!vals[i].equals("null")) {
// 构建 node 的左子节点:node.left 的值为 vals[i]
node.left = new TreeNode(Integer.parseInt(vals[i]));
// 将 node.left 入队
queue.add(node.left);
}
// 下标后移一位
i++;
// 若 vals[i] 不为 null
if (!vals[i].equals("null")) {
// 构建 node 的右子节点:node.left 的值为 vals[i]
node.right = new TreeNode(Integer.parseInt(vals[i]));
// 将 node.left 入队
queue.add(node.right);
}
// 下标后移一位
i++;
}
return root;
}
}