14、剑指 Offer 59 - I. 滑动窗口的最大值
一、题目
剑指 Offer 59 - I. 滑动窗口的最大值 难度困难
给定一个数组 nums 和滑动窗口的大小 k,请找出所有滑动窗口里的最大值。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
提示:
你可以假设 k 总是有效的,在输入数组不为空的情况下,1 ≤ k ≤ 输入数组的大小。
注意:本题与主站 239 题相同:https://leetcode-cn.com/problems/sliding-window-maximum/
二、解法
2.1、优先队列
核心思路
对于「最大值」,我们可以想到一种非常合适的数据结构,那就是优先队列(堆),其中的大根堆可以帮助我们实时维护一系列元素中的最大值。
对于本题而言,初始时,我们将数组 nums 的前 k 个元素放入优先队列中。每当我们向右移动窗口时,我们就可以把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中,在这种情况下,这个值在数组 nums 中的位置出现在滑动窗口左边界的左侧。因此,当我们后续继续向右移动窗口时,这个值就永远不可能出现在滑动窗口中了,我们可以将其永久地从优先队列中移除。
我们不断地移除堆顶的元素,直到其确实出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系,我们可以在优先队列中存储二元组 (num,index),表示元素 num 在数组中的下标为 index。
复杂度分析
时间复杂度:O(n log n),其中 n 是数组 nums 的长度。在最坏情况下,数组 nums 中的元素单调递增,那么最终优先队列中包含了所有元素,没有元素被移除。由于将一个元素放入优先队列的时间复杂度为 O(log n),因此总时间复杂度为 O(n log n)。
空间复杂度:O(n),即为优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的 O(n) 空间,只计算额外的空间使用。
Code
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// 边界条件 / 特殊情况
if (nums.length == 0 || k == 0) return new int[0];
int n = nums.length;
// 为了方便判断堆顶元素与滑动窗口的位置关系
// 我们在优先队列中存储二元组 (num,index),表示元素 num 在数组中的下标为 index。
PriorityQueue<int[]> queue = new PriorityQueue<int[]>(new Comparator<int[]>() {
public int compare(int[] pair1, int[] pair2) {
// 值是否相同?
// 如果不同,则根据数值大小来判断权重
// 如果相同,则根据索引大小来判断权重
return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
}
});
// 将数组 nums 的前 k 个元素放入优先队列中
for (int i = 0; i < k; ++i) {
queue.offer(new int[]{nums[i], i});
}
// answer
int[] ans = new int[n - k + 1];
// 第一个结果 -> 数组 nums 的前 k 个元素中的最大值 -> 大根堆的堆顶元素
ans[0] = queue.peek()[0];
// 循环处理剩下的元素
for (int i = k; i < n; ++i) {
// 把一个新的元素放入优先队列中
queue.offer(new int[]{nums[i], i});
// 去除出现在滑动窗口左边界的左侧的值,因为这个值永远不可能出现在滑动窗口中了
while (queue.peek()[1] <= i - k) {
queue.poll();
}
// 向 answer 中写入当前滑动窗口内的最大值
ans[i - k + 1] = queue.peek()[0];
}
return ans;
}
}
2.2、单调队列
核心思路
借助一个双端队列,存储单调递减的值,记作 deque。滑动窗口每向右移动一格,实时更新一次这个双端队列。如下图所示:
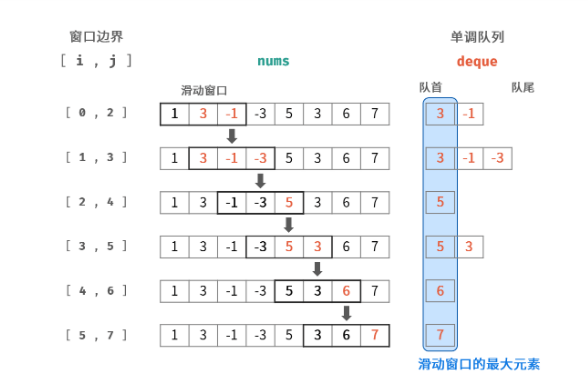
借助 deque 这个双端队列,我们可以将获取滑动窗口内最大值的时间复杂度从 O(k) 降低至 O(1),这也是本题的难点。
回忆 剑指Offer 30. 包含 min 函数的栈 ,其使用 单调栈 实现了随意入栈、出栈情况下的 O(1) 时间获取 “栈内最小值” 。本题同理,不同点在于 “出栈操作” 删除的是 “列表尾部元素” ,而 “窗口滑动” 删除的是 “列表首部元素” 。
复杂度分析
时间复杂度:O(n),其中 n 为数组 nums 长度;线性遍历 nums 占用 O(n) ;每个元素最多仅入队和出队一次,因此单调队列 deque 占用 O(2n) 。
空间复杂度:O(k) ,双端队列 deque 中最多同时存储 k 个元素(即窗口大小)。
Code
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// 边界条件 / 特殊情况
if (nums.length == 0 || k == 0) return new int[0];
// 双端队列 仅包含窗口内的元素,且严格
Deque<Integer> deque = new LinkedList<>();
// 答案
int[] answer = new int[nums.length - k + 1];
// 未形成窗口
for (int i = 0; i < k; i++) {
// 删除 deque 中所有小于 nums[i] 的元素
while (!deque.isEmpty() && deque.peekLast() < nums[i])
deque.removeLast();
// 向 deque 末尾添加新元素 nums[i]
deque.addLast(nums[i]);
}
// deque 的第一个元素即为当前窗口的最大值
answer[0] = deque.peekFirst();
// 形成窗口后
for (int i = k; i < nums.length; i++) {
// i-k 是已经在区间外了, 如果首位等于 nums[i-k], 那么说明此时首位值已经不再区间内了,需要删除
if (deque.peekFirst() == nums[i - k])
deque.removeFirst();
// 删除 deque 中所有小于 nums[i] 的元素
while (!deque.isEmpty() && deque.peekLast() < nums[i])
deque.removeLast();
// 向 deque 末尾添加新元素 nums[i]
deque.addLast(nums[i]);
// deque 的第一个元素即为当前窗口的最大值
answer[i - k + 1] = deque.peekFirst();
}
return answer;
}
}