29、剑指 Offer 20. 表示数值的字符串

無糖收录于系列 LeetCode-剑指offer-第二版-java

2021-10-03 2021-10-03 约 4112 字预计阅读 9 分钟

一、题目

剑指 Offer 20. 表示数值的字符串难度中等

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。

数值（按顺序）可以分成以下几个部分：

若干空格
一个小数或者整数
（可选）一个 'e' 或 'E' ，后面跟着一个整数
若干空格

小数（按顺序）可以分成以下几个部分：

（可选）一个符号字符（'+' 或 '-'）
下述格式之一：
1. 至少一位数字，后面跟着一个点 '.'
2. 至少一位数字，后面跟着一个点 '.' ，后面再跟着至少一位数字
3. 一个点 '.' ，后面跟着至少一位数字

整数（按顺序）可以分成以下几个部分：

（可选）一个符号字符（'+' 或 '-'）
至少一位数字

部分数值列举如下：

["+100", "5e2", "-123", "3.1416", "-1E-16", "0123"]

部分非数值列举如下：

["12e", "1a3.14", "1.2.3", "+-5", "12e+5.4"]

示例 1：

输入：s = "0"
输出：true

示例 2：

输入：s = "e"
输出：false

示例 3：

输入：s = "."
输出：false

示例 4：

输入：s = "    .1  "
输出：true

提示：

1 <= s.length <= 20
s 仅含英文字母（大写和小写），数字（0-9），加号 '+' ，减号 '-' ，空格 ' ' 或者点 '.' 。

二、解法

2.1、确定有限状态自动机（官方题解）

核心思路

预备知识

确定有限状态自动机（以下简称「自动机」）是一类计算模型。它包含一系列状态，这些状态中：

有一个特殊的状态，被称作「初始状态」。还有一系列状态被称为「接受状态」，它们组成了一个特殊的集合。其中，一个状态可能既是「初始状态」，也是「接受状态」。起初，这个自动机处于「初始状态」。随后，它顺序地读取字符串中的每一个字符，并根据当前状态和读入的字符，按照某个事先约定好的「转移规则」，从当前状态转移到下一个状态；当状态转移完成后，它就读取下一个字符。当字符串全部读取完毕后，如果自动机处于某个「接受状态」，则判定该字符串「被接受」；否则，判定该字符串「被拒绝」。

注意：如果输入的过程中某一步转移失败了，即不存在对应的「转移规则」，此时计算将提前中止。在这种情况下我们也判定该字符串「被拒绝」。

一个自动机，总能够回答某种形式的「对于给定的输入字符串 S，判断其是否满足条件 P」的问题。在本题中，条件 P 即为「构成合法的表示数值的字符串」。

自动机驱动的编程，可以被看做一种暴力枚举方法的延伸：它穷尽了在任何一种情况下，对应任何的输入，需要做的事情。

自动机在计算机科学领域有着广泛的应用。在算法领域，它与大名鼎鼎的字符串查找算法「KMP」算法有着密切的关联；在工程领域，它是实现「正则表达式」的基础。

问题描述

在 C++ 文档中，描述了一个合法的数值字符串应当具有的格式。具体而言，它包含以下部分：

符号位，即 ++、-− 两种符号整数部分，即由若干字符 0-90−9 组成的字符串小数点小数部分，其构成与整数部分相同指数部分，其中包含开头的字符 \text{e}e（大写小写均可）、可选的符号位，和整数部分相比于 C++ 文档而言，本题还有一点额外的不同，即允许字符串首末两端有一些额外的空格。

在上面描述的五个部分中，每个部分都不是必需的，但也受一些额外规则的制约，如：

如果符号位存在，其后面必须跟着数字或小数点。小数点的前后两侧，至少有一侧是数字。

思路与算法

根据上面的描述，现在可以定义自动机的「状态集合」了。那么怎么挖掘出所有可能的状态呢？一个常用的技巧是，用「当前处理到字符串的哪个部分」当作状态的表述。根据这一技巧，不难挖掘出所有状态：

起始的空格符号位整数部分左侧有整数的小数点左侧无整数的小数点（根据前面的第二条额外规则，需要对左侧有无整数的两种小数点做区分）小数部分字符 e 指数部分的符号位指数部分的整数部分末尾的空格下一步是找出「初始状态」和「接受状态」的集合。根据题意，「初始状态」应当为状态 1，而「接受状态」的集合则为状态 3、状态 4、状态 6、状态 9 以及状态 10。换言之，字符串的末尾要么是空格，要么是数字，要么是小数点，但前提是小数点的前面有数字。

最后，需要定义「转移规则」。结合数值字符串应当具备的格式，将自动机转移的过程以图解的方式表示出来：

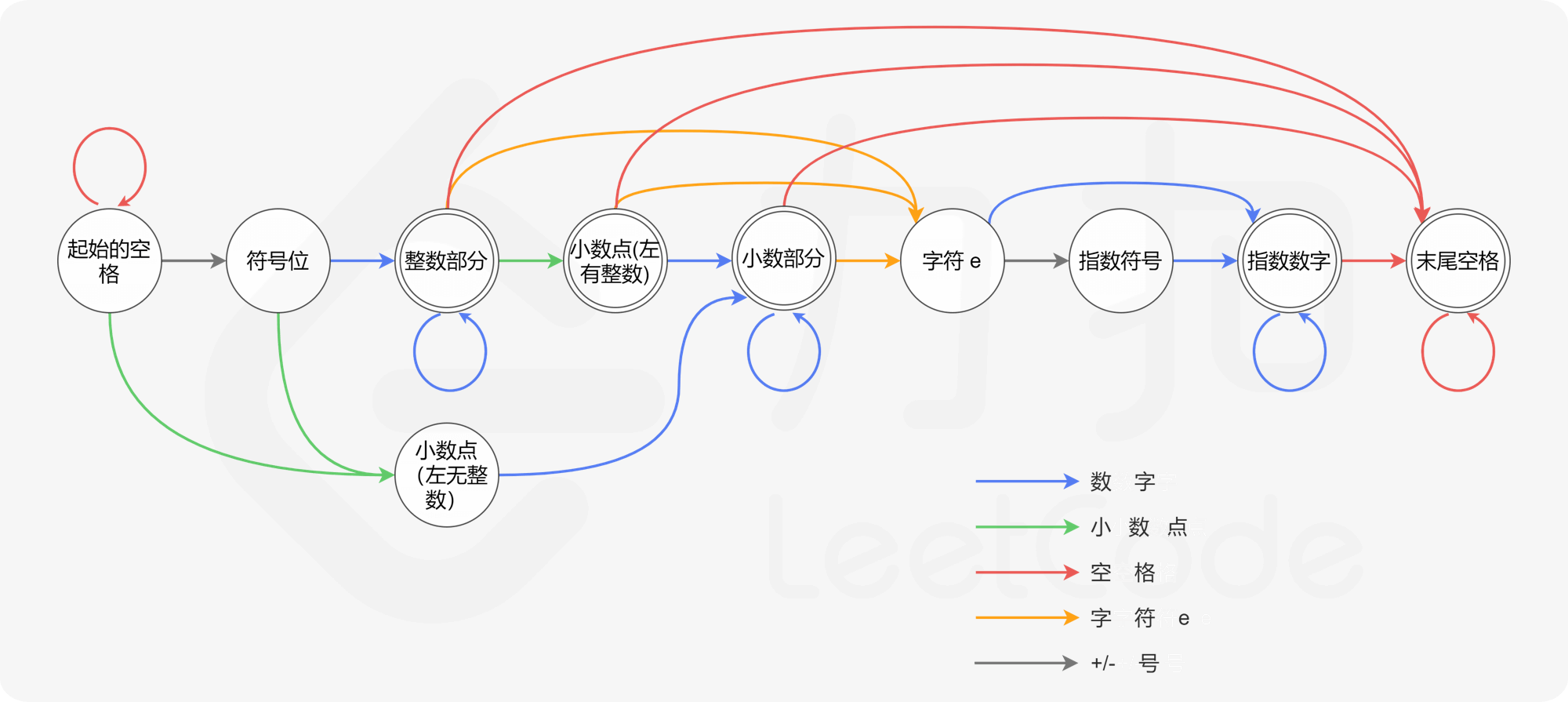
/post_images/image-20210913110127164.png

比较上图与「预备知识」一节中对自动机的描述，可以看出有一点不同：

我们没有单独地考虑每种字符，而是划分为若干类。由于全部 10 个数字字符彼此之间都等价，因此只需定义一种统一的「数字」类型即可。对于正负号也是同理。在实际代码中，我们需要处理转移失败的情况。例如当位于状态 1（起始空格）时，没有对应字符 e 的状态。为了处理这种情况，我们可以创建一个特殊的拒绝状态。如果当前状态下没有对应读入字符的「转移规则」，我们就转移到这个特殊的拒绝状态。一旦自动机转移到这个特殊状态，我们就可以立即判定该字符串不「被接受」。

复杂度分析

时间复杂度：O(n)，其中 n 为字符串的长度。我们需要遍历字符串的每个字符，其中状态转移所需的时间复杂度为 O(1)。

空间复杂度：O(1)，只需要创建固定大小的状态转移表。

Code：

class Solution {
    // 有限状态集合
    enum State {
        // 起始的空格
        STATE_INITIAL,
        // 整数部分符号位
        STATE_INT_SIGN,
        // 整数部分
        STATE_INTEGER,
        // 左侧有整数的小数点
        STATE_POINT,
        // 左侧无整数的小数点（根据前面的第二条额外规则，需要对左侧有无整数的两种小数点做区分）
        STATE_POINT_WITHOUT_INT,
        // 小数部分
        STATE_FRACTION,
        // 字符 e
        STATE_EXP,
        // 指数部分的符号位
        STATE_EXP_SIGN,
        // 指数部分的整数部分
        STATE_EXP_NUMBER,
        // 末尾的空格
        STATE_END
    }

    // 字符类型集合
    enum CharType {
        // 数字
        CHAR_NUMBER,
        // 字符 e
        CHAR_EXP,
        // 小数点
        CHAR_POINT,
        // 正负号
        CHAR_SIGN,
        // 空格
        CHAR_SPACE,
        // 非法字符
        CHAR_ILLEGAL
    }

    public boolean isNumber(String s) {
        // 状态机
        Map<State, Map<CharType, State>> transfer = new HashMap<State, Map<CharType, State>>();


        // 空格（初始状态） 的所有可转移状态
        Map<CharType, State> initialMap = new HashMap<CharType, State>() {{
            // 空格
            put(CharType.CHAR_SPACE, State.STATE_INITIAL);
            // 整数
            put(CharType.CHAR_NUMBER, State.STATE_INTEGER);
            // 小数点
            put(CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT);
            // 正负号
            put(CharType.CHAR_SIGN, State.STATE_INT_SIGN);
        }};
        transfer.put(State.STATE_INITIAL, initialMap);


        // 整数部分符号位 的所有可转移状态
        Map<CharType, State> intSignMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_INTEGER);
            put(CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT);
        }};
        transfer.put(State.STATE_INT_SIGN, intSignMap);


        // 整数部分 的所有可转移状态
        Map<CharType, State> integerMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_INTEGER);
            put(CharType.CHAR_EXP, State.STATE_EXP);
            put(CharType.CHAR_POINT, State.STATE_POINT);
            put(CharType.CHAR_SPACE, State.STATE_END);
        }};
        transfer.put(State.STATE_INTEGER, integerMap);

        // 左侧有整数的小数点 的所有可转移状态
        Map<CharType, State> pointMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_FRACTION);
            put(CharType.CHAR_EXP, State.STATE_EXP);
            put(CharType.CHAR_SPACE, State.STATE_END);
        }};
        transfer.put(State.STATE_POINT, pointMap);

        // 左侧无整数的小数点（根据前面的第二条额外规则，需要对左侧有无整数的两种小数点做区分) 的所有可转移状态
        Map<CharType, State> pointWithoutIntMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_FRACTION);
        }};
        transfer.put(State.STATE_POINT_WITHOUT_INT, pointWithoutIntMap);

        // 小数部分
        Map<CharType, State> fractionMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_FRACTION);
            put(CharType.CHAR_EXP, State.STATE_EXP);
            put(CharType.CHAR_SPACE, State.STATE_END);
        }};
        transfer.put(State.STATE_FRACTION, fractionMap);

        // 字符 e 的所有可转移状态
        Map<CharType, State> expMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
            put(CharType.CHAR_SIGN, State.STATE_EXP_SIGN);
        }};
        transfer.put(State.STATE_EXP, expMap);

        // 指数部分的符号位 的所有可转移状态
        Map<CharType, State> expSignMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
        }};
        transfer.put(State.STATE_EXP_SIGN, expSignMap);

        // 指数部分的整数部分 的所有可转移状态
        Map<CharType, State> expNumberMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
            put(CharType.CHAR_SPACE, State.STATE_END);
        }};
        transfer.put(State.STATE_EXP_NUMBER, expNumberMap);

        // 末尾的空格 的所有可转移状态
        Map<CharType, State> endMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_SPACE, State.STATE_END);
        }};
        transfer.put(State.STATE_END, endMap);


        int length = s.length();
        // 初始状态
        State state = State.STATE_INITIAL;

        // 循环处理每个字符, 模拟状态转移
        for (int i = 0; i < length; i++) {
            // 获取当前字符的类型
            CharType type = toCharType(s.charAt(i));

            if (!transfer.get(state).containsKey(type)) {
                return false;
            } else {
                state = transfer.get(state).get(type);
            }
        }
        return state == State.STATE_INTEGER || state == State.STATE_POINT || state == State.STATE_FRACTION || state == State.STATE_EXP_NUMBER || state == State.STATE_END;
    }

    // 获取字符的类型
    public CharType toCharType(char ch) {
        if (ch >= '0' && ch <= '9') {
            return CharType.CHAR_NUMBER;
        } else if (ch == 'e' || ch == 'E') {
            return CharType.CHAR_EXP;
        } else if (ch == '.') {
            return CharType.CHAR_POINT;
        } else if (ch == '+' || ch == '-') {
            return CharType.CHAR_SIGN;
        } else if (ch == ' ') {
            return CharType.CHAR_SPACE;
        } else {
            return CharType.CHAR_ILLEGAL;
        }
    }
}

2.2、确定有限状态自动机（评论区）

核心思路

本题使用有限状态自动机。根据字符类型和合法数值的特点，先定义状态，再画出状态转移图，最后编写代码即可。

字符类型：

空格「」、数字「 0—9 」、正负号「 +− 」、小数点「 . 」、幂符号「 eE 」。

状态定义：

按照字符串从左到右的顺序，定义以下 9 种状态。

开始的空格
幂符号前的正负号
小数点前的数字
小数点、小数点后的数字
当小数点前为空格时，小数点、小数点后的数字
幂符号
幂符号后的正负号
幂符号后的数字
结尾的空格

结束状态：

合法的结束状态有 2, 3, 7, 8 。

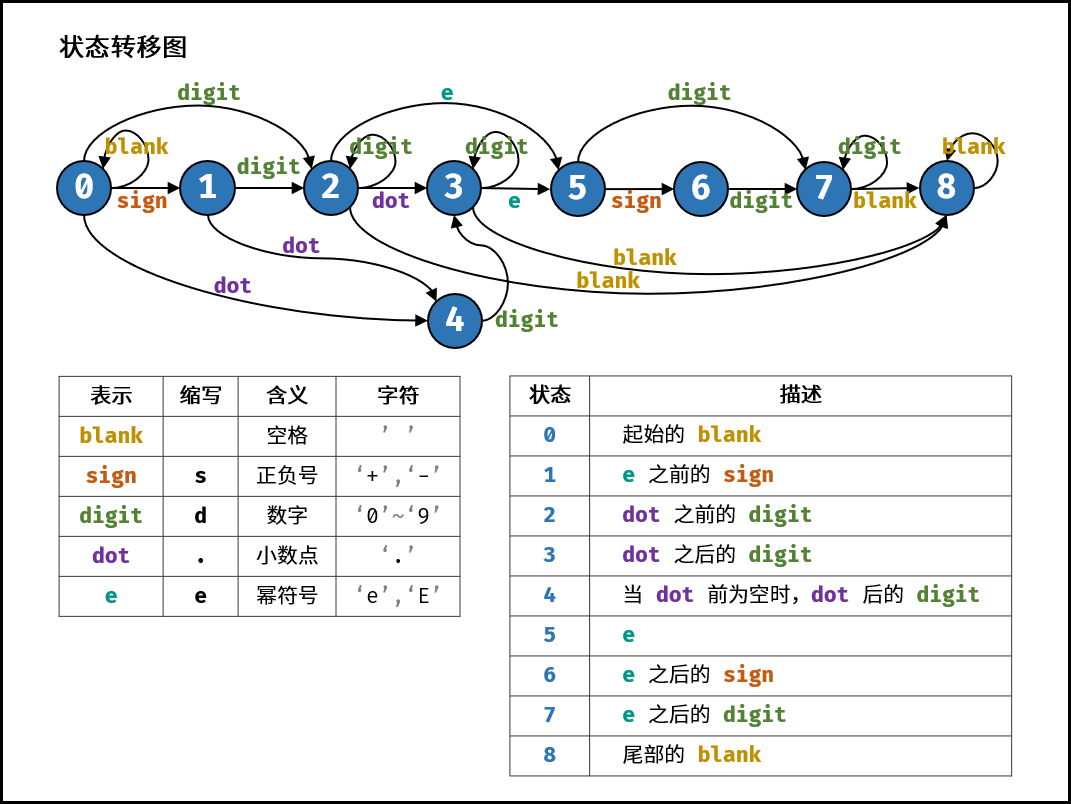
/post_images/image-20210913105508562.png

复杂度分析

时间复杂度：其中 N 为字符串 s 的长度，判断需遍历字符串，每轮状态转移的使用 O(1) 时间。

空间复杂度：states 和 p 使用常数大小的额外空间。

Code：

class Solution {
    public boolean isNumber(String s) {
        HashMap[] states = {
                new HashMap() {{ put(' ', 0); put('s', 1); put('d', 2); put('.', 4); }}, // 0. start with 'blank'
                new HashMap() {{ put('d', 2); put('.', 4); }},                           // 1. 'sign' before 'e'
                new HashMap() {{ put('d', 2); put('.', 3); put('e', 5); put(' ', 8); }}, // 2. 'digit' before 'dot'
                new HashMap() {{ put('d', 3); put('e', 5); put(' ', 8); }},              // 3. 'digit' after 'dot'
                new HashMap() {{ put('d', 3); }},                                        // 4. 'digit' after 'dot' (‘blank’ before 'dot')
                new HashMap() {{ put('s', 6); put('d', 7); }},                           // 5. 'e'
                new HashMap() {{ put('d', 7); }},                                        // 6. 'sign' after 'e'
                new HashMap() {{ put('d', 7); put(' ', 8); }},                           // 7. 'digit' after 'e'
                new HashMap() {{ put(' ', 8); }}                                         // 8. end with 'blank'
        };
        int p = 0;
        char t;
        for(char c : s.toCharArray()) {
            if(c >= '0' && c <= '9') t = 'd';       // digit
            else if(c == '+' || c == '-') t = 's';  // sign
            else if(c == 'e' || c == 'E') t = 'e';  // e or E
            else if(c == '.' || c == ' ') t = c;    // dot, blank
            else t = '?';                           // unknown
            if(!states[p].containsKey(t)) return false;
            p = (int)states[p].get(t);
        }
        return p == 2 || p == 3 || p == 7 || p == 8;
    }
}

2.3、常规解法

核心思路

什么有限状态自动机的我不太懂，常规解法可以做就不想搞这种可能只有这道题会用到的解法。

我首先想到的是判断否 false 而不是判断是 true，毕竟有这么多条件满足才能判断 true，但是只要有一个条件不满足就可以判断 false，最后代码的效率也还可以，那么接下来进入正题吧：

首先定义了四个flag，对应四种字符
- 是否有数字：hasNum
- 是否有e：hasE
- 是否有正负符号：hasSign
- 是否有点：hasDot
其余还定义了字符串长度 n 以及字符串索引 index
先处理一下开头的空格，index 相应的后移
然后进入循环，遍历字符串
- 如果当前字符 c 是数字：将 hasNum 置为 true ，index 往后移动一直到非数字或遍历到末尾位置；如果已遍历到末尾 ( index == n ) ，结束循环
- 如果当前字符 c 是 ’e’ 或 ‘E’ ：如果 e 已经出现或者当前 e 之前没有出现过数字，返回 fasle ；否则令 hasE = true ，并且将其他 3 个 flag 全部置为 false ，因为要开始遍历 e 后面的新数字了
- 如果当前字符 c 是 + 或-：如果已经出现过 + 或 - 或者已经出现过数字或者已经出现过 ‘.’ ，返回 flase ；否则令 hasSign = true
- 如果当前字符 c 是 ‘.’ ：如果已经出现过 ‘.’ 或者已经出现过 ’e’ 或 ‘E’ ，返回 false ；否则令 hasDot = true
- 如果当前字符 c 是 ’ ’ ：结束循环，因为可能是末尾的空格了，但也有可能是字符串中间的空格，在循环外继续处理
- 如果当前字符 c 是除了上面 5 种情况以外的其他字符，直接返回 false
处理空格，index 相应的后移
如果当前索引 index 与字符串长度相等，说明遍历到了末尾，但是还要满足 hasNum 为 true 才可以最终返回 true ，因为如果字符串里全是符号没有数字的话是不行的，而且 e 后面没有数字也是不行的，但是没有符号是可以的，所以 4 个 flag 里只要判断一下 hasNum 就行；所以最后返回的是 hasNum && index == n
如果字符串中间有空格，按以上思路是无法遍历到末尾的，index 不会与 n 相等，返回的就是 false

复杂度分析

时间复杂度：O(n)

空间复杂度：O(1)

Code：

class Solution {
    public boolean isNumber(String s) {
        int n = s.length();
        int index = 0;
        boolean hasNum = false, hasE = false;
        boolean hasSign = false, hasDot = false;
        while(index < n && s.charAt(index) == ' ')
            index++;
        while(index < n){
            while(index < n && s.charAt(index) >= '0' && s.charAt(index) <= '9'){
                index++;
                hasNum = true;
            }
            if(index == n){
                break;
            }
            char c = s.charAt(index);
            if(c == 'e' || c == 'E'){
                if(hasE || !hasNum){
                    return false;
                }
                hasE = true;
                hasNum = false; hasSign = false; hasDot = false;
            }else if(c == '+' || c == '-'){
                if(hasSign || hasNum || hasDot){
                    return false;
                }
                hasSign = true;
            }else if(c == '.'){
                if(hasDot || hasE){
                    return false;
                }
                hasDot = true;
            }else if(c == ' '){
                break;
            }else{
                return false;
            }
            index++;
        }
        while(index < n && s.charAt(index) == ' ')
            index++;
        return hasNum && index == n;
    }
}

REF

https://leetcode-cn.com/problems/biao-shi-shu-zhi-de-zi-fu-chuan-lcof/solution/biao-shi-shu-zhi-de-zi-fu-chuan-by-leetcode-soluti/

https://leetcode-cn.com/problems/biao-shi-shu-zhi-de-zi-fu-chuan-lcof/solution/mian-shi-ti-20-biao-shi-shu-zhi-de-zi-fu-chuan-y-2/

https://leetcode-cn.com/problems/biao-shi-shu-zhi-de-zi-fu-chuan-lcof/solution/jian-zhi-offer-20-biao-shi-shu-zhi-de-zi-060v/

目录

29、剑指 Offer 20. 表示数值的字符串

一、题目

剑指 Offer 20. 表示数值的字符串 难度中等

二、解法

2.1、确定有限状态自动机（官方题解）

核心思路

复杂度分析

Code：

2.2、确定有限状态自动机（评论区）

核心思路

复杂度分析

Code：

2.3、常规解法

核心思路

复杂度分析

Code：

REF

剑指 Offer 20. 表示数值的字符串难度中等