無糖的小宇宙
归档 分类 标签 专栏 系列 友链 关于
無糖的小宇宙

目录

27、剑指 Offer 17. 打印从1到最大的n位数

 收录于  系列 LeetCode-剑指offer-第二版-java
     约 2274 字   预计阅读 5 分钟 

一、题目

剑指 Offer 17. 打印从1到最大的n位数 难度简单

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

示例 1:

输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]

说明：

  • 用返回一个整数列表来代替打印
  • n 为正整数

二、解法

这道题在面试环节时，基本都要考察大数情况的。

2.1、迭代法

核心思路

由于本题要求返回 int 类型数组，相当于默认所有数字都在 int32 整型取值范围内，因此不考虑大数越界问题。

只需定义区间 $[1, 10^n - 1]$ 和步长 1 ，通过 for 循环生成结果列表并返回即可。

复杂度分析

时间复杂度：$O(10^n)$，生成长度为 $10^n$ 的列表需使用 $O(10^n)$ 时间。

空间复杂度： $O(1)$，建立列表需使用 $O(1)$ 大小的额外空间（ 列表作为返回结果，不计入额外空间 ）。

Code

class Solution {
    public int[] printNumbers(int n) {
        int end = (int)Math.pow(10, n) - 1;
        int[] answer = new int[end];
        for(int i = 0; i < end; i++) {
            answer[i] = i + 1;
        }
        return answer;
    }
}

2.2、大数打印解法

核心思路

实际上，本题的主要考点是大数越界情况下的打印。需要解决以下三个问题：

  1. 表示大数的变量类型 无论是 short / int / long … 任意变量类型，数字的取值范围都是有限的。因此，大数的表示应用字符串 String 类型。

  2. 生成数字的字符串集

  • 使用 int 类型时，每轮可通过 +1 生成下个数字，而此方法无法应用至 String 类型。并且， String 类型的数字的进位操作效率较低，例如 “9999” 至 “10000” 需要从个位到千位循环判断，进位 4 次。
  • 观察可知，生成的列表实际上是 n 位 0 - 9 的 全排列 ，因此可避开进位操作，通过递归生成数字的 String 列表。
  1. 递归生成全排列

基于分治算法的思想，先固定高位，向低位递归，当个位已被固定时，添加数字的字符串。例如当 n = 2 时（数字范围 1 - 99 ），固定十位为 0 - 9 ，按顺序依次开启递归，固定个位 0 - 9 ，终止递归并添加数字字符串。

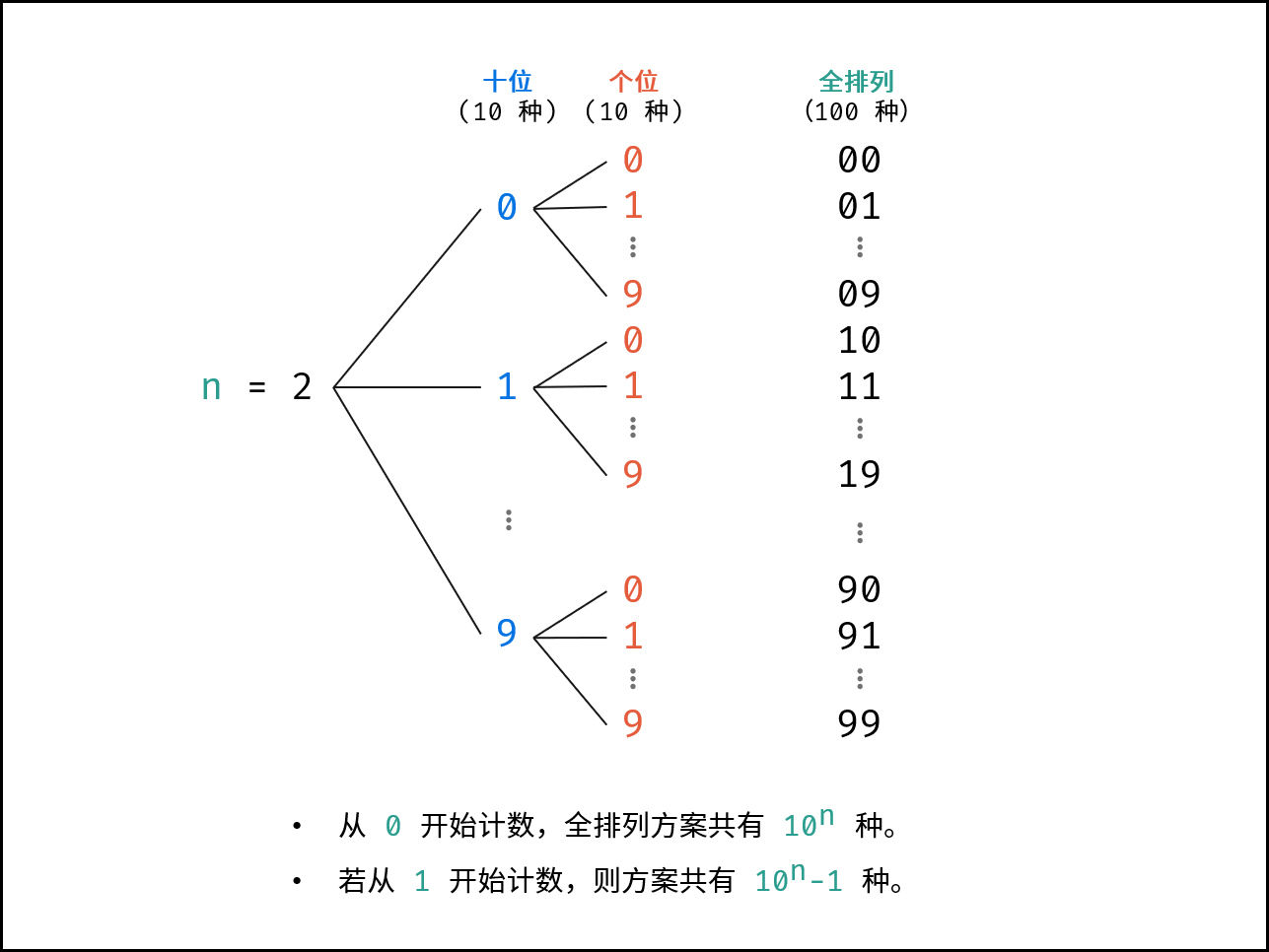
/post_images/image-20211011153020456.png

根据以上方法，可初步编写全排列代码：

class Solution {
    StringBuilder answer; // 解
    int n; // 题目给定的 n
    char[] num, charset = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'}; // num=缓冲区, charset=字符集

    public String printNumbers(int n) {
        this.n = n;
        answer = new StringBuilder(); // 数字字符串集
        num = new char[n]; // 定义长度为 n 的字符列表
        dfs(0); // 开启全排列递归
        answer.deleteCharAt(answer.length() - 1); // 删除最后多余的逗号
        return answer.toString(); // 转化为字符串并返回
    }

    void dfs(int x) {
        if (x == n) { // 终止条件：已固定完所有位
            answer.append(String.valueOf(num) + ","); // 拼接 num 并添加至 res 尾部，使用逗号隔开
            return;
        }
        for (char i : charset) { // 遍历 ‘0‘ - ’9‘
            num[x] = i; // 固定第 x 位为 i
            dfs(x + 1); // 开启固定第 x + 1 位
        }
    }
}

在此方法下，各数字字符串被逗号隔开，共同组成长字符串。返回的数字集字符串如下所示：

输入：n = 1
输出："0,1,2,3,4,5,6,7,8,9"

输入：n = 2
输出："00,01,02,...,10,11,12,...,97,98,99"

输入：n = 3
输出："000,001,002,...,100,101,102,...,997,998,999"

观察可知，当前的生成方法仍有以下问题：

  1. 诸如 00, 01, 02, ⋯ 应显示为 0, 1, 2, ⋯ ，即应 删除高位多余的 0 ;
  2. 此方法从 0 开始生成，而题目要求 列表从 1 开始 ；

以上两个问题的解决方法如下：

  1. 改造上述实现的 dfs(x) 函数

    • 令其成为“dfs(x,n) = 生成长度为 n 的数字字符串，当前正在确定下标为 x 的那一位”，这样可以将不同位长的数值全排列拆分出来。

    • 原先的 dfs(3) 要将 1~3 位的数值全排列全部计算出来，改造后将会拆分为 dfs(0,1)+dfs(0,2)+dfs(0,3)。

  2. 在字符集上做文章

    • 通过判断 dfs(x,n) 中 x 是否为 0 ，若是，说明当前还在固定下标为 0 的那一位, 即第一位数字（数值的最高位）,此时只需遍历字符集的 ‘1’~‘9’, 反之则遍历 ‘0’~‘9’

通过上述两个步骤，即可解决上述的两个问题。

复杂度分析

时间复杂度：$O(10^n)$，生成长度为 $10^n$ 的列表需使用 $O(10^n)$ 时间。

空间复杂度： $O(10^n)$，结果列表的长度为 $10^n-1$ ，各数字字符串的长度区间为 $1, 2, …, n$ ，因此占用 $O(10^n)$ 大小的额外空间。

Code

为 正确表示大数 ，以下代码的返回值为数字字符串集拼接而成的长字符串。

class Solution {
    // 解
    StringBuilder answer;
    // 字符集
    char[] chars = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
    // 缓冲区
    char[] num;

    public String printNumbers(int n) {
        // 结果
        answer = new StringBuilder();

        // 开启全排列递归
        for (int i = 1; i <= n; i++) {
            // 定义长度为 n 的字符数组缓冲区
            num = new char[i];
            // 生成长度为 n 的数字字符串，正在确定下标为 0 的那一位
            dfs(0, i);
        }

        // 删除最后多余的逗号
        answer.deleteCharAt(answer.length() - 1);
        // 转化为字符串并返回
        return answer.toString();
    }

    // 生成长度为 n 的数字字符串，当前正在确定下标为 x 的那一位（缓冲区 num 的数组下标）
    void dfs(int x, int n) {
        // 终止条件：已固定完所有位
        if (x == n) {
            // 拼接 num 并添加至 res 尾部，使用逗号隔开
            answer.append(String.valueOf(num) + ",");
            return;
        }

        // 去除前导0：若当前还在固定下标为 0 的那一位, 则说明是第一位数字（即数值最高位）, 只遍历字符集的 '1'~'9', 反之则遍历 '0'~'9'
        int start = (x == 0) ? 1 : 0;
        for (int index = start; index < chars.length; index++) {
            // 固定第 x 位为 i, 对应到缓冲区下标为 x-1
            num[x] = chars[index];
            // 开启固定第 x + 1 位
            dfs(x + 1, n);
        }
    }
}

本题要求输出 int 类型数组。为 运行通过 ，可在添加数字字符串 s 前，将其转化为 int 类型。代码如下所示：

class Solution {
    // 当前已求解数字个数, 作为游标使用
    int count = 0;
    // 解
    int[] answer;

    // 字符集
    char[] chars = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
    // 缓冲区
    char[] num;

    public int[] printNumbers(int n) {
        // 根据解的已知个数初始化空间
        answer = new int[(int) Math.pow(10, n) - 1];

        // 开启全排列递归
        for (int i = 1; i <= n; i++) {
            // 定义长度为 n 的字符数组缓冲区
            num = new char[i];
            // 生成长度为 n 的数字字符串，正在确定下标为 0 的那一位
            dfs(0, i);
        }

        // 转化为字符串并返回
        return answer;
    }

    // 生成长度为 n 的数字字符串，当前正在确定下标为 x 的那一位（缓冲区 num 的数组下标）
    void dfs(int x, int n) {
        // 终止条件：已固定完所有位
        if (x == n) {
            // 将缓冲区的字符串转换为 int , 加入解
            answer[count++] = Integer.parseInt(String.valueOf(num));
            return;
        }

        // 去除前导0：若当前还在固定下标为 0 的那一位, 则说明是第一位数字（即数值最高位）, 只遍历字符集的 '1'~'9', 反之则遍历 '0'~'9'
        int start = (x == 0) ? 1 : 0;
        for (int index = start; index < chars.length; index++) {
            // 固定第 x 位为 i, 对应到缓冲区下标为 x-1
            num[x] = chars[index];
            // 开启固定第 x + 1 位
            dfs(x + 1, n);
        }
    }
}

REF

https://leetcode-cn.com/problems/da-yin-cong-1dao-zui-da-de-nwei-shu-lcof/solution/mian-shi-ti-17-da-yin-cong-1-dao-zui-da-de-n-wei-2/

更新于 2021-10-01
 大数, 全排列
返回 | 主页